探究两点直线方程的推导与应用（从点到直线）

数学作为一门抽象的学科，既具有理论性又具有实践性。而两点直线方程的推导与应用是数学中的基础知识之一，它能够帮助我们更好地理解直线的性质与特点，并且在实际问题中有着广泛的应用。本文将从两点直线方程的推导方法入手，逐步展开相关内容，带领读者深入了解这一数学概念。

通过两点确定直线的必要性

1.1直线是一种基本几何图形

1.2两点确定一条直线的直观理解

斜率是推导两点直线方程的关键

2.1斜率的定义和性质

2.2两点之间的斜率如何计算

点斜式方程的推导与应用

3.1点斜式方程的基本形式

3.2通过斜率和一点确定直线方程

截距式方程的推导与应用

4.1截距的概念和计算

4.2通过截距和斜率确定直线方程

一般式方程的推导与应用

5.1一般式方程的基本形式

5.2通过斜率和截距确定直线方程

两点直线方程的应用举例

6.1直线与曲线的交点问题

6.2直线的平行和垂直关系判定

两点直线方程的实际应用

7.1建模问题中的直线方程应用

7.2直线方程在物理学中的应用

两点直线方程的变形与扩展

8.1垂线与斜率的关系

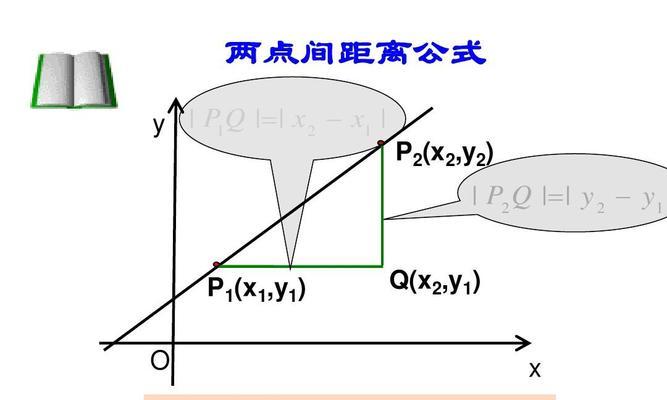
8.2点到直线的距离公式推导

两点直线方程的局限性与拓展

9.1引入参数化的直线方程

9.2直线方程在三维空间中的推广

两点直线方程的重要性与应用前景

通过以上几个部分的详细阐述，我们深入探究了两点直线方程的推导与应用。从直观理解两点确定直线的必要性开始，逐步引入斜率的概念，推导出点斜式方程、截距式方程和一般式方程。我们给出了两点直线方程在实际问题中的应用举例，展示了它在不同领域的作用。接着，我们探讨了两点直线方程的变形与拓展，揭示了它们在更广阔的数学领域中的应用前景。通过本文的学习，读者可以更好地理解和应用两点直线方程，为解决实际问题提供更多的数学思维和方法。